This is the second article in a three-part series that reviews the thermal, optical, and mechanical properties of glass. We will define common glass properties and explain their application and importance in component design.
We often hear from engineers who are evaluating the impact of a design change from one lens material to another. For example, they may be switching from an existing polycarbonate lens design to glass due to concerns about durability in harsh environments. They ask “Can I use my existing lens design with the new glass material? Will the resulting light output have the same chromaticity, distribution, and intensity?” The answers to these questions are rooted in understanding the optical properties of materials.
The optical properties of a material determine how it will interact with light. Today, most engineers use advanced software tools to simulate the properties of a material and their impact on optical performance. Still, familiarity with a few fundamental optical properties will help engineers pick the right material for their application. In this article, we review refractive index, transmission, absorption, and wavelength dependency and discuss how these properties impact product design.
Refractive Index
You’re probably familiar with the concept of “traveling at the speed of light”, but did you know that the speed of light can change? Light’s speed is reduced when it travels through a medium due to the interaction of photons with electrons. Typically, higher electron densities in a material result in lower velocities. This is why light travels fast in glass, faster in water, and fastest in a vacuum. The refractive index (n) of a material is defined as the ratio of the speed of light in a vacuum to that of light in the material.
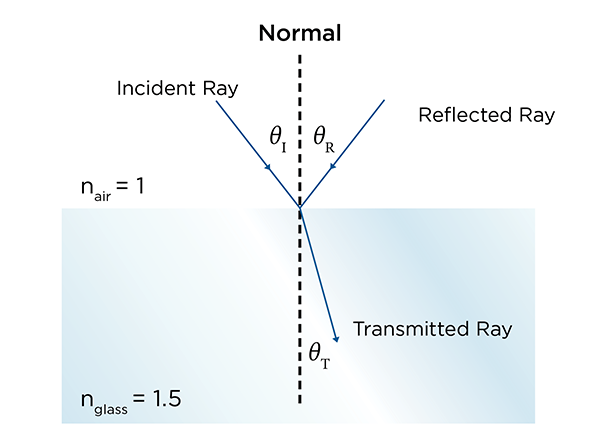
When a beam of light hits a glass surface, part of the beam is reflected and part is transmitted. The index of refraction of the glass determines not only how much light is reflected and transmitted, but also its refracted angle in the glass. The angle of transmission can be calculated using Snell’s law:
Larger indices of refraction in glass result in greater differences between the angle of incidence and transmission of light. The reflection of light at the surface occurs due to an instantaneous change in refractive index between glass and its surrounding medium. For normal incidence (Θi = 0°), the amount of light reflected is found by
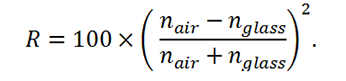
For most glasses with a refractive index of 1.5, reflection losses at the surface result in an approximate 4% decrease in light intensity.
Application:
When designing a lens that transmits light, it is necessary to consider the material’s refractive index. Even a small change in the refractive index can affect the candela distribution of the transmitted light. This can be seen in the example below, where light travels through two identically shaped plano convex lenses with different refractive indices.
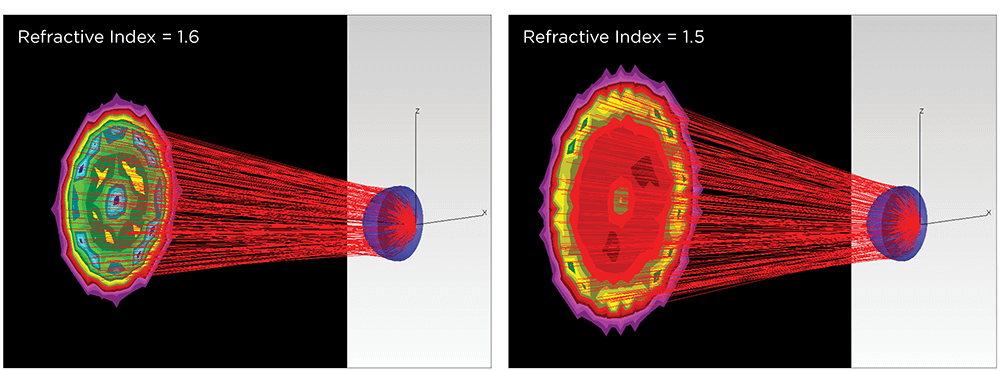
The luminous intensity distribution on the right is from a glass lens with a typical refractive index of 1.5.Displayed on the left, a lens with a refractive index of 1.6.It could be made from a higher index of refraction glass or plastic, such as polycarbonate. For an application that requires light illumination across a larger surface area, it may be better to choose a glass with a smaller refractive index. Or for instance, you want to obtain more intensity closer to the center of the candela distribution; you would choose a material with a higher refractive index. Understanding this optical property will provide you with one more tool to help you select the right material and achieve your desired performance results.
Absorption
When light travels through a glass, the intensity of the light is typically reduced. This absorption happens when the energy of a photon of light matches the energy needed to excite an electron within the glass to its higher energy state, and the photon is absorbed by the glass.
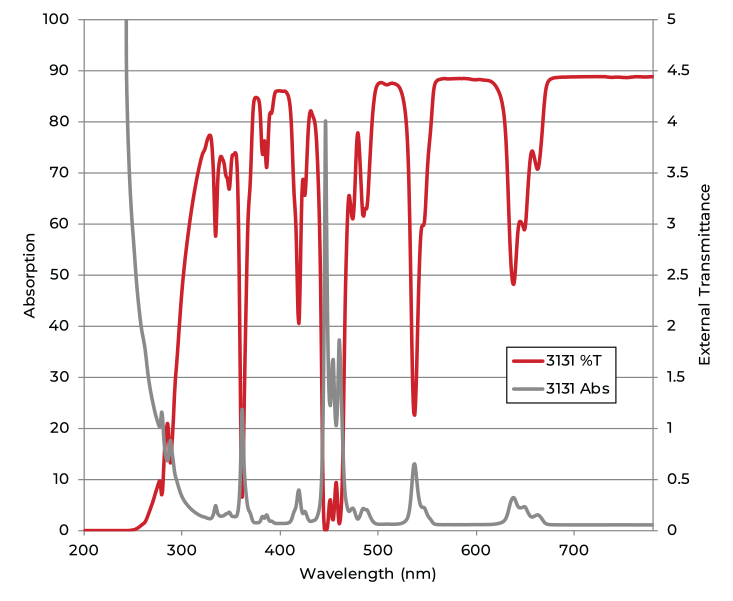
The absorbance of a glass, shown in the figure above as a function of wavelength, is often used to describe the decrease in intensity of light as it travels through the glass. It is defined as
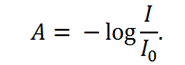
This value depends on the composition and thickness of the glass as well as the wavelength of incident light.
Application:
Rare earth glass filters are often used to calibrate the absorption and transmittance of spectrophotometers. These glasses absorb light at very specific wavelengths, which enable the calibration of well characterized absorption peaks across the ultraviolet, visible, and infrared spectrums.
In some applications it is beneficial to reduce light output in equal parts across all wavelengths. Neutral density filters, for example, absorb all wavelengths nearly equally and are often used in photography to reduce the intensity of light without affecting the color. They’re also used to attenuate lasers and other light sources where the power can’t be adjusted or reduced.
Transmission/Transmittance
Any light that is not absorbed by a glass or reflected at its surface will be transmitted through the glass. It is often very important to know exactly how much light will pass through a glass at specified wavelengths. Often, glasses are discussed in terms of their transmittance or transmission. The same information is provided by both of these terms but transmission is reported with ranges from 0 % to 100 % and transmittance from 0 to 1.
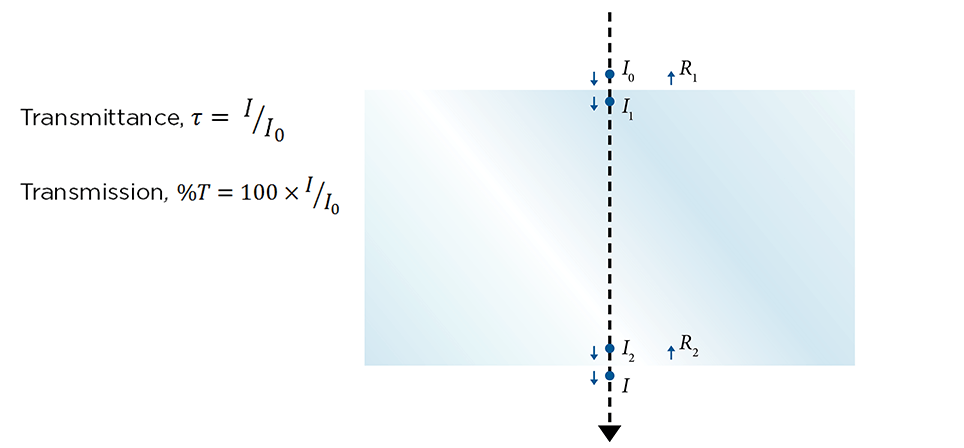
The transmittance is also often reported as internal transmission and defined as:
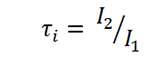
External transmittance includes both the absorption loss of the material and the loss of light due to reflection at the two glass surfaces, while the internal transmittance only includes absorption losses of the material.
Application:
The reporting of transmittance values of a material can vary depending on the application or common industry nomenclature. While most industrial glasses report optical properties as external transmittance, values for filter glasses are typically given as internal transmittance. This is because filter glasses may be treated with anti-reflective coatings to prevent intensity losses at the glass surface. For example, a glass filter which has an external transmission of 92% at 589.2 nm might have a much higher internal transmittance of 0.98, as is the case with our 3131 filter.
When reviewing a glass property sheet and designing a part, it’s important to know if the industry specifications you’re trying to meet are for external transmission or internal transmittance. For instance, many of the Federal Aviation Administration (FAA) specifications for airport and aerospace applications have requirements that are provided in external transmission. SAE Aerospace Standard AS 25050 requires specific external transmission ratios for the different colored ware. Depending on the transmission level, various grades (A-D) are assigned to the ware.
Wavelength Dependence of Values
It’s important to note that all of the optical properties previously outlined are wavelength dependent. For example, the refractive index of a glass increases as the wavelength of incident light gets shorter. The dispersion of the refractive index is often shown using the example of white light splitting while traveling through a prism. According to Snell’s law, since nblue > nred, light with blue wavelengths refract or change directions more while red wavelengths refract less as they enter, travel though, and leave surfaces of different matter.
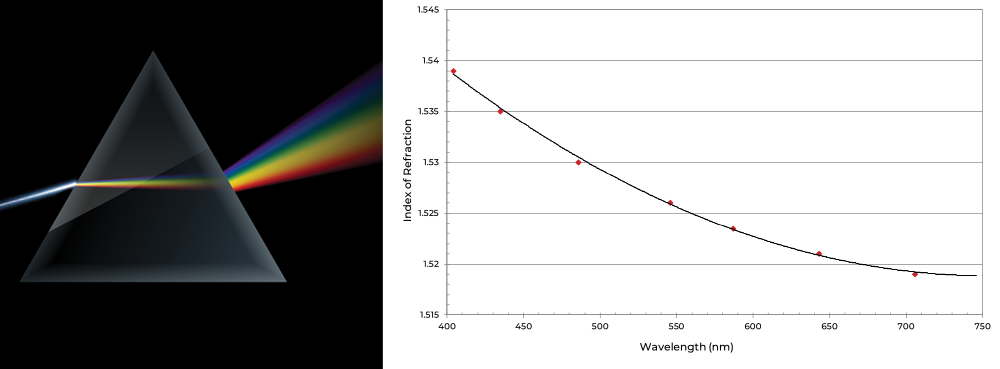
The wavelength dependence of the refractive index is often described using the empirical Cauchy equation,
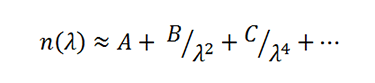
here A, B, and C are constants specific to the glass composition. This relationship works well for visible wavelengths, but often does not accurately describe ultraviolet or infrared behavior.
The reflection, absorption, and transmission of a glass also vary with wavelength. The color of a glass is determined by the wavelengths that the glass absorbs and transmits. For example, a glass that absorbs green, yellow, and red wavelengths and transmits blue wavelengths will appear blue to the eye. Chromaticity is something we know a lot about and will discuss in greater detail in a future blog article.
Application:
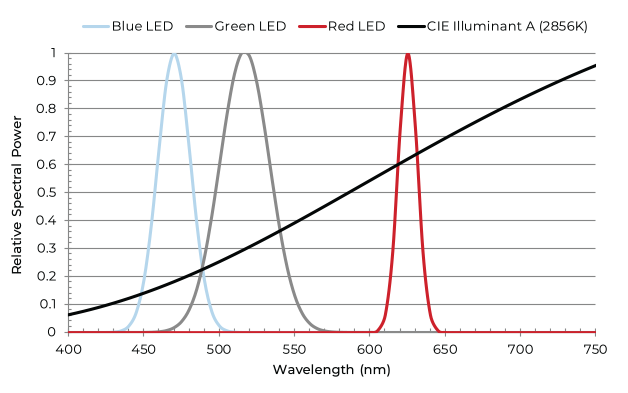
As LED adoption increases and replaces conventional light sources, it is important to consider how their light output differs. The image below shows how the spectral power varies between a blue, green, and red LED compared to an incandescent (CIE Illuminant A) source. Colored LEDs have narrow wavelength bands of emitted light which must be considered when designing for specific application wavelengths.
For example, if you are designing optical prisms or other features of a lens, it is critical to choose the correct index of refraction. As previously mentioned, the index of refraction changes with wavelength, so it may be necessary to address any index changes and design optical features that work across the spectrum with LEDs that range from blue to green to red.
So far in this series we’ve discussed thermal and optical properties of glass and their impact to product design. These are just two elements of successful design. Our final article in this series will explore the mechanical properties of glass, which are especially relevant when products are used in harsh environments or are subject to corrosive chemicals.
Learn More About Glass
To help you design better-performing glasses lenses, we created a comprehensive eBook that includes more than 40 pages of information on the thermal, optical, and mechanical properties of glass.
If you want to learn how to design glass lenses and components that are optimized for both your performance requirements and operating environment, download our free eBook.

